Non-Linear Structural Design
P-Delta Analysis
By Amer Mezher, P.Eng. 2023- 02-14
1. what is P-Delta Effect ?
It is one type of geometric nonlinearity involves the equilibrium compatibility relationships of a structural system loaded about its deflected configuration. Of particular concern is the application of gravity load on laterally displaced multi-story building structures. This condition magnifies story drift and certain mechanical behaviors while reducing deformation capacity.
P-Delta effect typically involves large external forces upon relatively small displacements. If deformations become sufficiently large as to break from linear compatibility relationships, then Large-Displacement and/or Large-Deformation analyses may become necessary. The two sources of P-Delta effect are illustrated in Figure 1, and described as follows:
1. P_ Delta about column
_ P-δ effect, or P-“small-delta”, is associated with local deformation relative to the element chord between end nodes. Small P-delta effects can affect overall structural behavior by slightly reducing the buckling load and can change the moment within the member.
Typically, P-δ only becomes significant at larger displacement values or in especially slender columns. Small P-delta effect is important for local buckling and for design algorithms that expect member buckling to be accounted for by analysis. This includes the AISC direct-analysis method.
Small P-delta is automatically included in frame elements to the extent that the deflected shape can be well represented by a cubic curve. The frame small P-delta effect is very accurate for a single element with effective-length factor of 2 (cantilever), and it is moderately accurate for an effective-length factor of 1 (pinned or sway condition). When accurate small P-delta effects are important for analysis or design of a member, it is generally recommended to auto-mesh frame objects into 2 or more elements, especially for axial loads close to buckling. For most other purposes, small P-delta effects as they impact the overall structure are adequately considered with a single frame object between connections.
_ P-Δ effect, or P-“big-delta”, is associated with displacements of the member ends. Large P-delta effect is important for overall structure behavior under significant axial load. As indicated intuitively by Figure 2, gravity loading will influence structural response under significant lateral displacement.
P-Δ may contribute to loss of lateral resistance, ratcheting of residual deformations, and dynamic instability. As shown in Figure 3, effective lateral stiffness decreases, reducing strength capacity in all phases of the force-deformation relationship. To consider P-Δ effect directly, gravity load should be present during nonlinear analysis. Application will cause minimal increase to computational time and will remain accurate for drift levels up to 10%.
Large P-delta is included in all elements – frame, shell, solid, link.
2. P – Delta about structure
3. P-Δ![]() on F-D relationship (PEER/ATC 2010)
on F-D relationship (PEER/ATC 2010)
2. How to include P-Delta effect in analysis ?
The two primary means for including P-Delta effect in nonlinear analysis include:
1. For each load combination, create a nonlinear analysis case which includes the P-Delta geometric-nonlinearity parameter.
2. For the gravity loads anticipated, create an Initial P-Delta Analysis case which includes the P-Delta geometric-nonlinearity parameter, then consider all other analyses as linear while using the stiffness matrix developed for this one set of P-Delta loads.
3. What are the types of P-Delta analysis ?
1. Simply supported beam P-δ 2. Cantilevered column P-δ 3. Cantilevered column P-∆
1. Simply supported beam P-δ
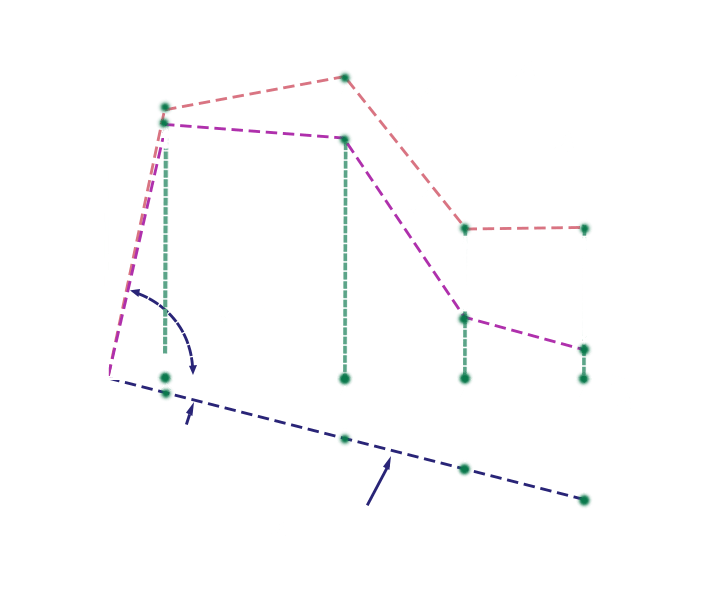
P-δ is a local effect associated with axial load on displacement relative to element chord extending between end nodes. Figure 1 illustrates the influence of P-δ on a simply supported beam. Here, a longitudinal distributed load ω correlates with elastic bending-stiffness properties KE to induce vertical displacement δ. An additional flexural contribution comes from the relationship between this deformed configuration and axial load P.
Values for the maximum flexural response which occurs at element midspan are shown in Figure 3 :
(A). Structural configuration
(B). Displaced configuration
(C). Elastic stiffness contribution
(D). Geometric stiffness contribution
(E). Total moment
3. P-δ applied to a simply supported beam
2. Cantilevered column P-δ
Now, when observing P-δ effect on a cantilevered column, response is shown in Figure 4 :
4. P-∆ applied to a cantilevered column
However, columns seldom displace with single curvature. More commonly, especially with multi-story-building analysis and design, columns deform according to a third order (cubic) displacement pattern under double curvature. As shown in Figure 4. , P-δ effect is much less pronounced because an inflection point intersects the element chord near midspan, previously where displacement from chord was greatest.

5. P-∆ applied to a cantilevered column
3. Cantilevered column P-∆
However, what is often of significance, given this loading condition and double-curvature displacement pattern, is P-∆ effect. Although displacement deviates from element chord much less, the lateral displacement associated with story drift is significant. With increasing levels of drift, gravity load has a greater effect on mechanical behavior, as shown in Figure 6. P-∆ effect should be implemented during design, whether static or dynamic, linear or nonlinear.
6. P-∆ applied to a cantilevered column
5. References
- Wilson, E. L. (2004). Static and Dynamic Analysis of Structures (4th ed.). Berkeley, CA: Computers and Structures, Inc.
- Powell, G. H. (2010). Modeling for Structural Analysis: Behavior and Basics (1st ed.). Berkeley, CA: Computers and Structures, Inc.
- Deierlein, G. G., Reinhorn, A. M., and Willford, M. R. (2010). Nonlinear Structural Analysis For Seismic Design, NEHRP Seismic Design Technical Brief No. 4., NIST GCR 10-917-5. Gaithersburg, MD: National Institute of Standards and Technology.
- PEER/ATC (2010). Modeling and acceptance criteria for seismic design and analysis of tall buildings, PEER/ATC 72-1 Report. Redwood City, CA: Applied Technology Council.

